Circular Binaries
two compact objects in circular orbits
About circular binaries
When compact object binaries emit gravitational waves, the loss of energy and angular momentum tends to make the binary orbit more and more circular. We think that most of the binaries observed by detectors like LIGO will have very close to circular orbits. Gravitational wave signals from circular binaries have been very well studied. As many of the features of circular binaries will carry over to more complicated situations (e.g., spinning binaries, eccentric binaries), they will serve as our starting point for our exploration of gravitational wave signals and sounds.
Here, we will assume that both of our compact objects (let's say they are black holes) are each moving in a circular orbit about the binary's center of mass. We will assume each black hole is not spinning about its own axis. We will ignore the merger of the black holes, as that contributes very little to the sound (see our discussion of this under "The Basics").
To get a better visual sense of the systems we are exploring on this page, consider the following two animations by Ankit Singh and P. Ajith. They show the orbital motion and waveforms of two black holes. The first movie shows an equal mass system (m1=m2=10 solar masses). The second shows an unequal mass one (m1=4, m2=16 solar masses).
Here, we will assume that both of our compact objects (let's say they are black holes) are each moving in a circular orbit about the binary's center of mass. We will assume each black hole is not spinning about its own axis. We will ignore the merger of the black holes, as that contributes very little to the sound (see our discussion of this under "The Basics").
To get a better visual sense of the systems we are exploring on this page, consider the following two animations by Ankit Singh and P. Ajith. They show the orbital motion and waveforms of two black holes. The first movie shows an equal mass system (m1=m2=10 solar masses). The second shows an unequal mass one (m1=4, m2=16 solar masses).
Effect of total mass and mass ratio
For circular binaries, there are two important numbers that determine the overall behavior of the system, the masses of each black hole (m1 and m2). In particular, the gravitational wave signal is most affected by the total mass, M=m1+m2 and the mass ratio q=m1/m2 (with m1<m2). Let's explore how this affects the sound of the signal.
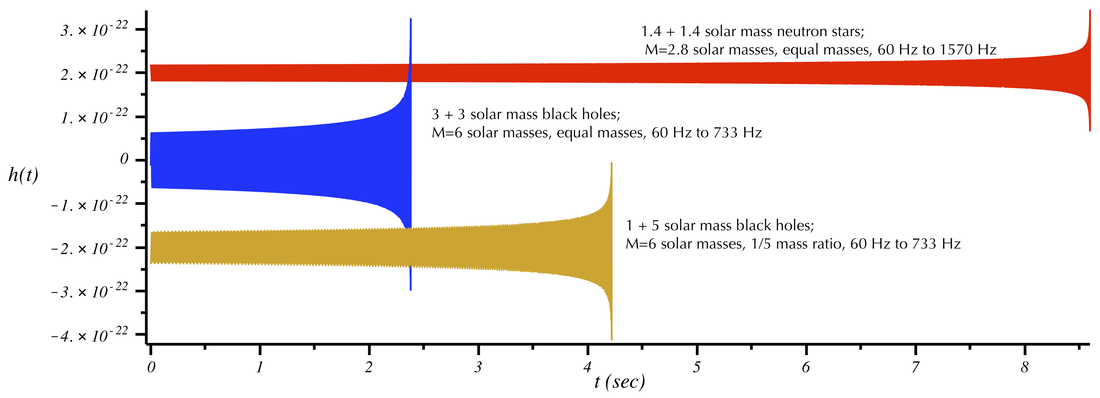
The figure below shows the gravitational-wave signal from three different compact object binaries: The red curve represents two binary neutron stars, each with the same mass (equal to 1.4 times the Sun's mass). The blue curve represents a more massive system consisting of two black holes each with a mass 3 times our Sun. Just like a larger organ pipe produces lower-frequency sounds than a narrow pipe, the more massive binary system (6 vs. 2.8 solar masses) produces waves at lower frequencies. Because this system is heavier, its frequencies occur at lower values. Notice also that although both curves start at the same frequency (60 Hz at t=0 s), the red curve (binary neutron stars) has a longer time duration. This is because (i) the lighter mass system radiates gravitational waves with less intensity and (ii) the merger occurs at a higher frequency (which this system takes longer to reach). The gold-colored curve shows another black hole binary system with the same total mass as the blue curve, but with unequal masses. Because the total mass is the same, the curve ends at the same frequency (this will vary slightly in a full simulation that incorporates the merger). However, because the masses are unequal the rate that gravitational-wave energy is emitted is slower, so the system takes longer to decay and reach the merger frequency around 733 Hz.
Play with the sound files below the figure and listen for yourself!
The figure below shows the gravitational-wave signal from three different compact object binaries: The red curve represents two binary neutron stars, each with the same mass (equal to 1.4 times the Sun's mass). The blue curve represents a more massive system consisting of two black holes each with a mass 3 times our Sun. Just like a larger organ pipe produces lower-frequency sounds than a narrow pipe, the more massive binary system (6 vs. 2.8 solar masses) produces waves at lower frequencies. Because this system is heavier, its frequencies occur at lower values. Notice also that although both curves start at the same frequency (60 Hz at t=0 s), the red curve (binary neutron stars) has a longer time duration. This is because (i) the lighter mass system radiates gravitational waves with less intensity and (ii) the merger occurs at a higher frequency (which this system takes longer to reach). The gold-colored curve shows another black hole binary system with the same total mass as the blue curve, but with unequal masses. Because the total mass is the same, the curve ends at the same frequency (this will vary slightly in a full simulation that incorporates the merger). However, because the masses are unequal the rate that gravitational-wave energy is emitted is slower, so the system takes longer to decay and reach the merger frequency around 733 Hz.
Play with the sound files below the figure and listen for yourself!
Harmonics of the signal (a bit more advanced material)
When you listened to the unequal mass system above, you might have noticed that--in addition to lasting twice as long as the equal mass binary black hole--the system sounds a bit "richer". This is because unequal mass systems have additional complexity called higher harmonics. (This discussion will be a bit more technical, so feel free to move on to spinning or elliptical binaries when you've had enough.)
Vibrating systems in nature typically have a natural frequency and corresponding "pattern" to their oscillation, which usually depends on their shape or materials. This is called the fundamental mode. For a guitar string, this depends on the length of the string and the speed at which vibrations propagate along the string. (This speed depends on the string's tension and mass per unit length.) In addition, physical systems will often vibrate at multiples of the fundamental frequency. These are called harmonics. The fundamental is often (but not always) the first harmonic (i.e., the lowest frequency of all the harmonics). (Also, the fundamental frequency is usually more easily excited to a large amplitude.)
For merging black holes or neutron stars, the harmonics are multiples of the orbital frequency (which is determined by the binary separation and the total mass). The fundamental mode for circular binaries is at twice the orbital frequency, 2 forb. This is the primary frequency component that you hear in the above sounds. However, there are other frequency components as well that are much lower in amplitude. For equal mass binaries, harmonics arise at even integer multiples, 4 forb, 6 forb, 8 forb, etc. For unequal-mass binaries additional harmonics enter the picture at odd integer multiples 1 forb, 3 forb, 5 forb, etc. In particular, the "second loudest" harmonics (after the fundamental at 2 forb) are the harmonics at 1 forb, 3 forb. This is the source of the "richer" sound for the third binary (gold curve) above. You can clearly hear a lower frequency component and the fact that there is more than one "tone" present. Because both even and odd multiples are present, the sound is slightly dissonant (much like simultaneously playing two adjacent keys on a piano). Let's explore this a bit more.
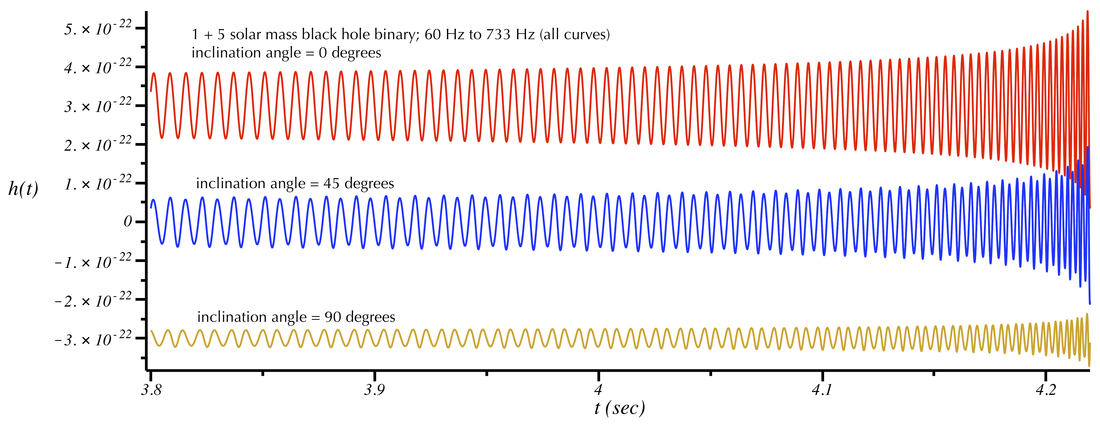
In addition to the mass ratio, the other parameter that affects what harmonics are present is the binary inclination angle. This is the angle between the detector (e.g., LIGO) and the "axis" of the orbital plane (i.e., the "normal" to the orbital plane). The strength of the different harmonics that are present in the signal vary for binaries with different inclination angles. Consider these three waveforms which differ only in the inclination angle:
Vibrating systems in nature typically have a natural frequency and corresponding "pattern" to their oscillation, which usually depends on their shape or materials. This is called the fundamental mode. For a guitar string, this depends on the length of the string and the speed at which vibrations propagate along the string. (This speed depends on the string's tension and mass per unit length.) In addition, physical systems will often vibrate at multiples of the fundamental frequency. These are called harmonics. The fundamental is often (but not always) the first harmonic (i.e., the lowest frequency of all the harmonics). (Also, the fundamental frequency is usually more easily excited to a large amplitude.)
For merging black holes or neutron stars, the harmonics are multiples of the orbital frequency (which is determined by the binary separation and the total mass). The fundamental mode for circular binaries is at twice the orbital frequency, 2 forb. This is the primary frequency component that you hear in the above sounds. However, there are other frequency components as well that are much lower in amplitude. For equal mass binaries, harmonics arise at even integer multiples, 4 forb, 6 forb, 8 forb, etc. For unequal-mass binaries additional harmonics enter the picture at odd integer multiples 1 forb, 3 forb, 5 forb, etc. In particular, the "second loudest" harmonics (after the fundamental at 2 forb) are the harmonics at 1 forb, 3 forb. This is the source of the "richer" sound for the third binary (gold curve) above. You can clearly hear a lower frequency component and the fact that there is more than one "tone" present. Because both even and odd multiples are present, the sound is slightly dissonant (much like simultaneously playing two adjacent keys on a piano). Let's explore this a bit more.
In addition to the mass ratio, the other parameter that affects what harmonics are present is the binary inclination angle. This is the angle between the detector (e.g., LIGO) and the "axis" of the orbital plane (i.e., the "normal" to the orbital plane). The strength of the different harmonics that are present in the signal vary for binaries with different inclination angles. Consider these three waveforms which differ only in the inclination angle:
Inspiral of 1 solar mass and 5 solar mass black holes, with varying inclination angles. Only the last half second of the corresponding audio is displayed. Note that the indicated frequency range refers to the fundamental harmonic.
(Headphones or good speakers are recommended to appreciate the subtle differences in the above sounds.)
From the waveforms and the three sounds files above, notice the following: the sound has a "richer" mixture of frequencies as the inclination is increased. In particular, you can hear a stronger lower frequency component in the last sound (this corresponds to the harmonic at 1 forb. Notice also that the amplitude of the signal gets smaller as the inclination gets closer to 90 degrees.
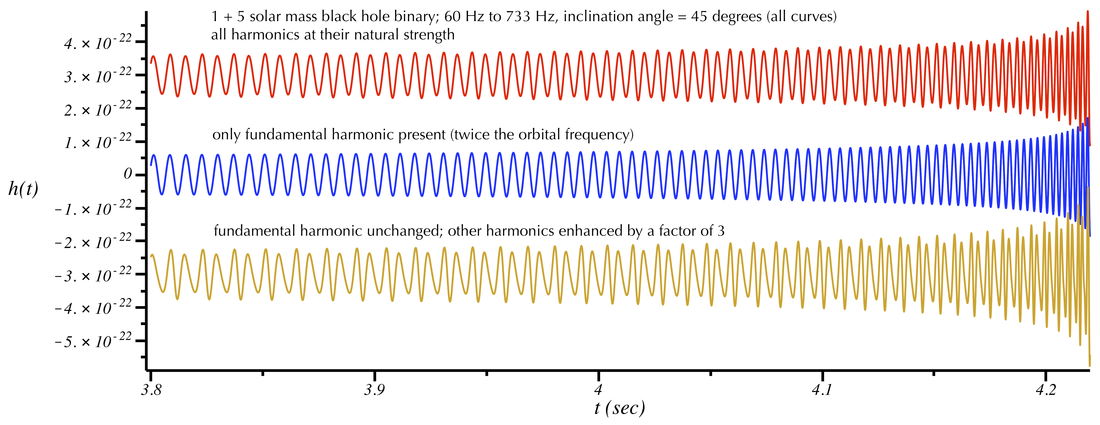
To explore this concept in more detail, we can try to artificially manipulate the signal to enhance or suppress the various harmonics. (Headphones or good speakers are again recommended.) In the plot below we show the gravitational-wave signal from the same system as above, choosing an inclination angle of 45 degrees. The top (red) curve shows the physically correct waveform. In the middle (blue) curve shows signal that only includes the fundamental harmonic at 2 forb. The bottom (gold) curve shows a signal in which the fundamental harmonic is unchanged, but the higher harmonics are enhanced by a factor of 3.
From the waveforms and the three sounds files above, notice the following: the sound has a "richer" mixture of frequencies as the inclination is increased. In particular, you can hear a stronger lower frequency component in the last sound (this corresponds to the harmonic at 1 forb. Notice also that the amplitude of the signal gets smaller as the inclination gets closer to 90 degrees.
To explore this concept in more detail, we can try to artificially manipulate the signal to enhance or suppress the various harmonics. (Headphones or good speakers are again recommended.) In the plot below we show the gravitational-wave signal from the same system as above, choosing an inclination angle of 45 degrees. The top (red) curve shows the physically correct waveform. In the middle (blue) curve shows signal that only includes the fundamental harmonic at 2 forb. The bottom (gold) curve shows a signal in which the fundamental harmonic is unchanged, but the higher harmonics are enhanced by a factor of 3.
Inspiral of 1 solar mass and 5 solar mass black holes, artificially varying the harmonic structure. Only the last half second of the corresponding audio is displayed.
Try listening to the above three sounds (works better with headphones). Notice that the middle sound (blue curve) sounds "more pure." The third sound (gold curve), for which the harmonics besides the fundamental are enhanced, has noticeably more frequency components than either of the other two signals.
Ok, now it's time to explore elliptical binaries.
Ok, now it's time to explore elliptical binaries.
Notes on waveform model used to produce sounds on this page:
The sounds on this page used a post-Newtonian (PN) model accurate to 3PN order in the phasing and 2PN order in the amplitude (see Blanchet, Living Reviews 2014, Sec. 9.4). The compact objects are nonspinning and assumed to lie 100 Mpc from Earth. Sky localization angles in the detector antenna pattern functions are taken to be Theta=Phi=0. The polarization angle is Psi=pi/6. Only the inspiral is considered and the calculation is stopped at an upper frequency corresponding to the innermost stable circular orbit (ISCO).
The sounds on this page used a post-Newtonian (PN) model accurate to 3PN order in the phasing and 2PN order in the amplitude (see Blanchet, Living Reviews 2014, Sec. 9.4). The compact objects are nonspinning and assumed to lie 100 Mpc from Earth. Sky localization angles in the detector antenna pattern functions are taken to be Theta=Phi=0. The polarization angle is Psi=pi/6. Only the inspiral is considered and the calculation is stopped at an upper frequency corresponding to the innermost stable circular orbit (ISCO).
