Spinning Binaries
exploring spin and precession
About spin
While gravity only depends on an object's mass in Newton's theory, in Einstein's theory of General Relativity all forms of mass and energy affect the curvature of spacetime. This includes the spin of an object. For example, the Earth spins about the axis through its North and South poles at a rate of once per day. General Relativity predicts that along with its mass, the Earth's spin rate also affects the gravity around our planet. This influences the orbits of satellites and has been measured by the Gravity Probe- B and LAGEOS experiments.
Black holes and neutron stars in a binary system can both spin very rapidly. The resulting effects on the orbital motion of the binary can be significant. In addition, the details of how gravitational radiation is produced also depends on the spin of the two compact stars. The spin of a body thus imprints itself on the gravitational wave signal. There are two main effects that we will explore here: (i) Spinning systems radiate gravitational wave energy at different rates depending on how the spins are oriented with respect to the orbital plane of the binary. (ii) When the spins are not aligned with the orbital plane axis, both the orbital plane itself and the individual spins can precess. (Much like a spun-up top will precess.) This precession can impart interesting modulations on the gravitational-wave signal.
Black holes and neutron stars in a binary system can both spin very rapidly. The resulting effects on the orbital motion of the binary can be significant. In addition, the details of how gravitational radiation is produced also depends on the spin of the two compact stars. The spin of a body thus imprints itself on the gravitational wave signal. There are two main effects that we will explore here: (i) Spinning systems radiate gravitational wave energy at different rates depending on how the spins are oriented with respect to the orbital plane of the binary. (ii) When the spins are not aligned with the orbital plane axis, both the orbital plane itself and the individual spins can precess. (Much like a spun-up top will precess.) This precession can impart interesting modulations on the gravitational-wave signal.
Aligned spins
First, let's assume we have two black holes (m1 = 1 and m2 = 3 solar masses) and consider the case where all the spins in the system are aligned or anti-aligned. For example, consider an x-y-z coordinate system. The angular momentum of the binary orbit will point along +z axis (the direction perpendicular to the plane of the orbit). The individual spins of each black hole will point in either the +z or -z directions. The "spin" refers here to a dimensionless number which can range from 0 to 1 for black holes (spin = 1 is the fastest that black holes can spin). The sign of the spin determines if the spin axis points in the +z or -z direction. Here are the waveforms for a few different configurations, followed by their corresponding sounds:
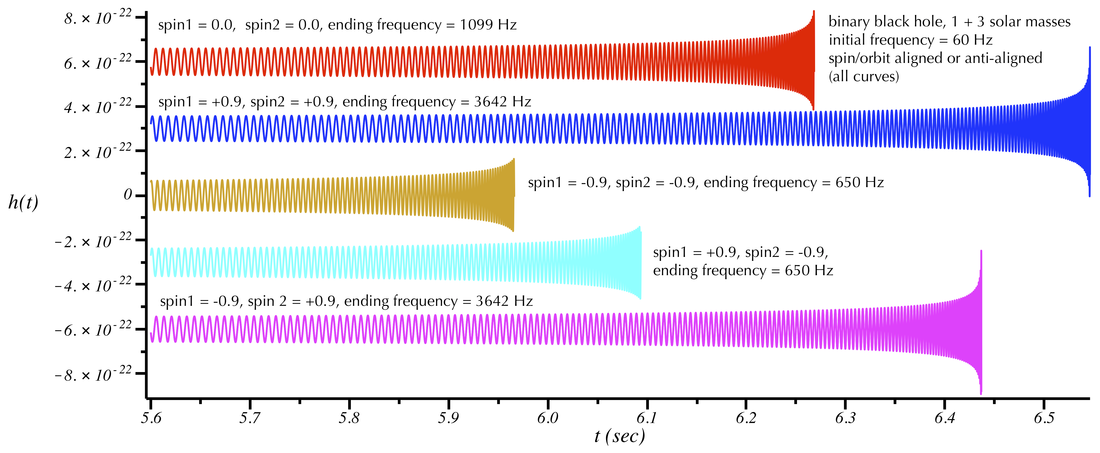
Gravitational wave signals from pairs of inspiralling black holes with different spins. There is no precession and the spins are either aligned or anti-aligned with the axis of orbital motion. Spin1 refers to the 1 solar mass black hole. Spin2 refers to the 3 solar mass black hole. All signals start from 60 Hz.
The main thing to notice here is that when the spin of the larger black hole is "up" (+z direction, along the orbital angular momentum direction), the duration of the signal is longer and the frequencies it reaches are higher. When the larger black hole spin is in the -z direction, the inspiral ends at a lower frequency and the overall signal has a slightly smaller duration. (The orbital angular momentum is a quantity like spin that is associated with the direction of the orbital motion. Black holes orbiting counter-clockwise in the x-y plane have an orbital angular momentum in the +z direction.)
You can get a visual sense of what is happening in these aligned-spin systems from this animation by Ankit Singh and P. Ajith. It shows two black holes with equal masses that are both spinning, with the spins oriented in the -z direction (opposite the orbital angular momentum). The orbital motion looks qualitatively like that for a circular orbit. When aligned in the +z or -z direction, the magnitude of the spins primarily affects the duration of the signal, it's frequency at merger, and the rate at which the signal sweeps from low frequencies to high frequencies.
You can get a visual sense of what is happening in these aligned-spin systems from this animation by Ankit Singh and P. Ajith. It shows two black holes with equal masses that are both spinning, with the spins oriented in the -z direction (opposite the orbital angular momentum). The orbital motion looks qualitatively like that for a circular orbit. When aligned in the +z or -z direction, the magnitude of the spins primarily affects the duration of the signal, it's frequency at merger, and the rate at which the signal sweeps from low frequencies to high frequencies.
Precessing spins
Now for the interesting case. Let's assume that the spins of each black hole are not aligned with the axis of the orbital motion (i.e., they are not along the +z or -z directions initially). This will break the symmetry that was present in the above situation. Because the spin of an object (as well as its mass) couples to spacetime, there is a "dragging of spacetime" that occurs in Einstein's theory. The "direction" associated with this dragging is perpendicular to the spin-axis of each black hole. (The effect exists for all spinning masses, but is most dramatic for black holes, so we will focus on those objects to simplify the discussion.) Each spinning black hole "drags" the space around it, and its companion feels the effect of this distortion to the spacetime geometry. This affects the orbital motion of each member of the binary.
The primary effect is to make the orbital plane precess. This introduces a modulation to the amplitude of the signal, and this modulation is easily heard in the "sound" of the GW signal. The modulation happens at a rate that is slower than the orbital period. The details depend on many quantities, including the magnitude and direction of the spins of each black hole and the orientation and sky-position of the binary with respect to the GW detector.
In addition to the effect on the "direction" of the orbital plane, the spin of each black hole also affects the spin of its companion. In addition to the precession of the orbital plane, the spins of the individual black holes will also precess. For example, as the Earth revolves around the Sun, its spin axis remains pointed in a fixed direction in space over long periods of time. However, the gravitational tugs of the Moon and the Sun cause the Earth's spin axis to precess on very long timescales, with a period of 26,000 years. This is an effect of Newtonian gravity. General relativity introduces new effects (discussed in the previous paragraphs) that cause a similar precession of the spin directions. For black holes in close orbits, this precession can happen very quickly.
To get a visual idea of what is happening, consider the following animation by Ankit Singh and P. Ajith:
The primary effect is to make the orbital plane precess. This introduces a modulation to the amplitude of the signal, and this modulation is easily heard in the "sound" of the GW signal. The modulation happens at a rate that is slower than the orbital period. The details depend on many quantities, including the magnitude and direction of the spins of each black hole and the orientation and sky-position of the binary with respect to the GW detector.
In addition to the effect on the "direction" of the orbital plane, the spin of each black hole also affects the spin of its companion. In addition to the precession of the orbital plane, the spins of the individual black holes will also precess. For example, as the Earth revolves around the Sun, its spin axis remains pointed in a fixed direction in space over long periods of time. However, the gravitational tugs of the Moon and the Sun cause the Earth's spin axis to precess on very long timescales, with a period of 26,000 years. This is an effect of Newtonian gravity. General relativity introduces new effects (discussed in the previous paragraphs) that cause a similar precession of the spin directions. For black holes in close orbits, this precession can happen very quickly.
To get a visual idea of what is happening, consider the following animation by Ankit Singh and P. Ajith:
You can clearly see that the plane of the motion quickly deviates from its initial orientation. You can also see that the spin vectors (the arrows indicating the spin directions and relative magnitudes) initially remain roughly fixed in orientation but then start to precess. This precession becomes very dramatic as the merger is approached. Notice the modulations that are imparted to the gravitational-wave signal in the right-hand panel. More details can be found at this page.
Another nice animation from the SXS numerical relativity collaboration shows a spinning system modeled using the full equations of general relativity. The effects of orbital plane precession and the precession of the individual spins are clearly seen. This animation includes the merger of the two black holes:
Another nice animation from the SXS numerical relativity collaboration shows a spinning system modeled using the full equations of general relativity. The effects of orbital plane precession and the precession of the individual spins are clearly seen. This animation includes the merger of the two black holes:
Sounds from precessing binaries [this section under active development...stay tuned]
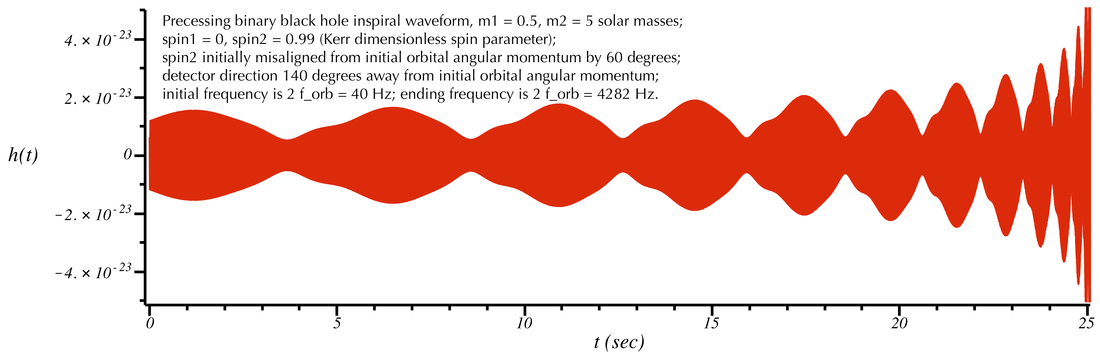
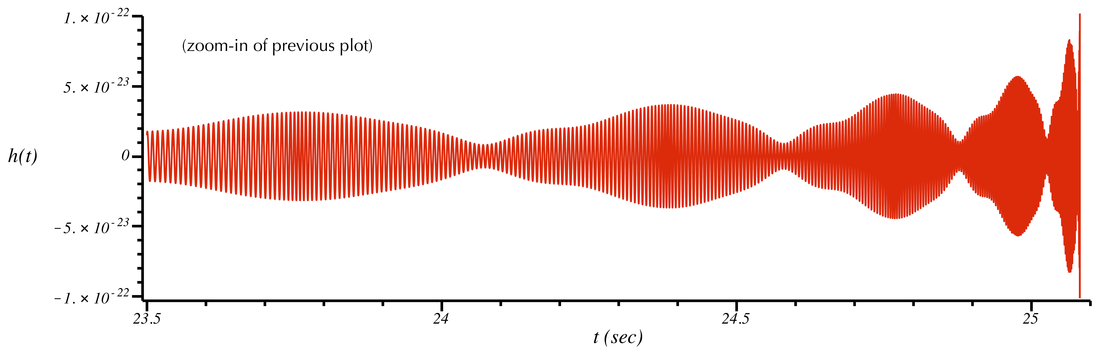
We have not yet had time to complete a thorough exploration of this rich topic. For now we show one (particularly dramatic) example of the GW signal from a spinning, precessing binary. This system starts at a frequency of 2 f_orb = 40 Hz. The black hole masses are m1=0.5, m2=5 solar masses. The smaller black hole is not spinning, but the larger one has a spin of 0.99 times the maximum value possible for a black hole. The spin is initially misaligned from the orbital plane axis by 60 degrees. (The orbital plane initially points in the +z direction.) The GW detector is located 140 degrees away from the +z direction. The plots below show the signal, with the second plot zooming-in to the last few seconds before merger. The sound of this signal follows the plots.
Inspiral signal of two black holes showing extreme precession. System parameters are listed on the plot. Only one black hole is spinning (at close to the maximum rate). Notice the large modulations to the amplitude of the signal.
Zoom-in of the above plot showing the final few seconds. Notice that in addition to the amplitude modulations, there are phase modulations as well. These can be clearly heard in the sound file below.
The above sound displays several interesting features. As in the case of all inspiralling binaries, there is an overall tendency for the frequency and amplitude to increase as the merger is approached. However, spin introduces two additional kinds of modulations to the signal that are clearly audible. The first is an amplitude modulation. This is clearly seen in both plots above, and can be heard as a fluctuating component to the "volume" of the sound. In addition, there is a phase modulation as well (this can only be seen in the second plot). Whereas for non-spinning binaries the frequency evolves in a monotonic way (always increasing), for spinning binaries the rate at which the frequency evolves fluctuates. For example, near t = 23.75 s, 24.4 s, and 24.75 s one can see (and hear) that the frequency of the sound suddenly increases and then decreases.
This sound illustrates the depth of information that can be carried by a gravitational-wave signal. We will extend our exploration of spin effects on this page in the near future.
This sound illustrates the depth of information that can be carried by a gravitational-wave signal. We will extend our exploration of spin effects on this page in the near future.
Notes on waveform model used to produce sounds on this page.
The sound above was based on a model for spinning, circular binaries that implements the equations from a classic paper by Apostolatos, Cutler, Sussman, and Thorne [Phys. Rev. D, 49, 6274, (1994)]. The equations of motion there were supplemented by several higher-order spin effects. [In the sound file the first 1.5 seconds were removed relative to the plotted waveform due to an apparent glitch in our numerical integration of the equations. Interestingly, it was by listening to the sound of the signal that we were able to discover this issue.]
The sound above was based on a model for spinning, circular binaries that implements the equations from a classic paper by Apostolatos, Cutler, Sussman, and Thorne [Phys. Rev. D, 49, 6274, (1994)]. The equations of motion there were supplemented by several higher-order spin effects. [In the sound file the first 1.5 seconds were removed relative to the plotted waveform due to an apparent glitch in our numerical integration of the equations. Interestingly, it was by listening to the sound of the signal that we were able to discover this issue.]
