Elliptical Binaries
exploring ellipticity, radiation reaction, and periastron precession
About elliptical orbits
So far we've explored circular orbits. But generally, stars will have orbits that are elliptical---their paths trace out ellipses. This is what we will explore here. (We will assume the compact objects don't spin about their axes so all the effects we discuss will only depend on the ellipticity.)
The ellipse is characterized by two numbers: (i) its "width;" this tells us how big the orbit is. This is usually specified by the semi-major axis of the ellipse (half its width along the "long" end). For orbiting binary stars, the period of one orbit also gives us this information (if we know the total mass). (ii) The other important number for an ellipse is its eccentricity e. This tells us how "elliptical" it is: e=0 is a circle and e=0.99999.... is an extremely elongated ellipse (one axis is much shorter than the other).
When compact objects have elliptical orbits, the gravitational-wave (GW) signal becomes much more complex for several reasons:
The ellipse is characterized by two numbers: (i) its "width;" this tells us how big the orbit is. This is usually specified by the semi-major axis of the ellipse (half its width along the "long" end). For orbiting binary stars, the period of one orbit also gives us this information (if we know the total mass). (ii) The other important number for an ellipse is its eccentricity e. This tells us how "elliptical" it is: e=0 is a circle and e=0.99999.... is an extremely elongated ellipse (one axis is much shorter than the other).
When compact objects have elliptical orbits, the gravitational-wave (GW) signal becomes much more complex for several reasons:
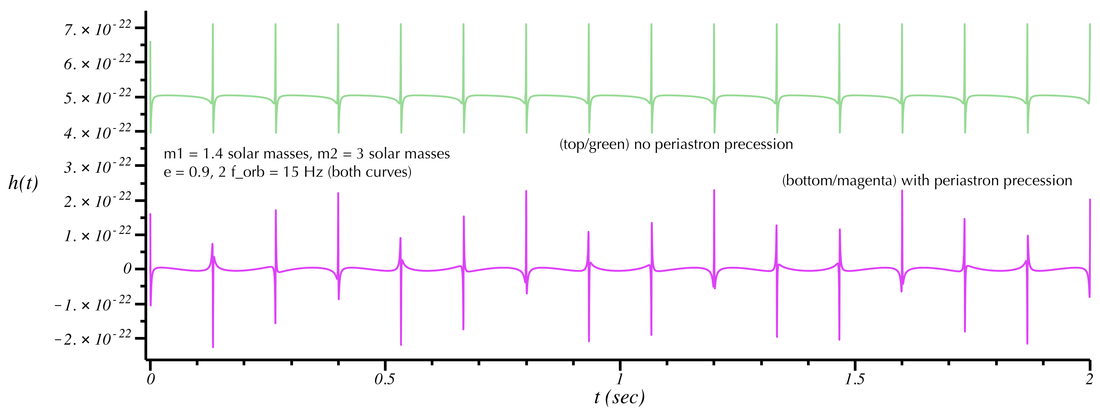
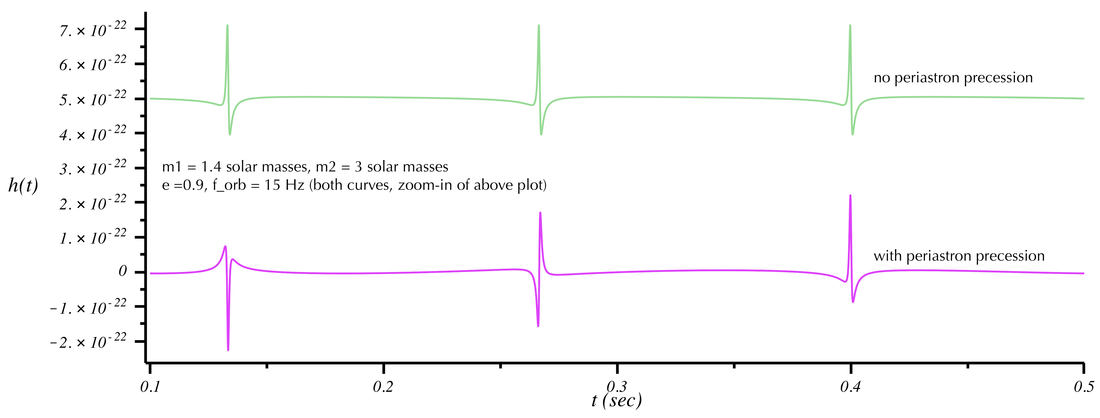
- Unlike circular orbits, the stars moves at different speeds during a single orbit---faster when they are at periastron (the point of closest approach) and slower when they are at apastron (the point where the stars are farthest apart). For highly eccentric orbits the difference in speeds is extreme, resulting in a "spiky" GW signal (as opposed to a smooth sinusoid as in circular orbits). Because these spikes are not at all sinusoidal, the corresponding "sound" contains many frequency components. The "spike" near periastron in particular is associated with a "knocking" sound. The "knocks" arrive at the orbital period of the binary, but the "knocking sound" itself is at a much higher frequency (and is really a sound composed of several frequencies). A circular orbit (that is not inspiralling via GW emission) consists of a pure tone at twice the orbital frequency (plus the much weaker harmonics at multiples of that frequency as discussed in the circular binaries page). However, GWs from eccentric orbits have a distribution of frequencies, and the strongest (or "loudest") frequency depends on the value of the eccentricity e.
- When the effects of general relativity are included, the perfect elliptical orbits predicted by Newtonian gravity are modified. The ellipses precess around in the orbital plane. The elliptical orbit "path" no longer forms a closed curve (except when the orbital period and periastron advance period form an integer ratio). This is called "periastron precession" and was the first effect predicted by Einstein's theory. Mercury's orbit experiences a small periastron precession due to this relativistic effect; Einstein's theory was able to precisely explain its magnitude. (Note that there is also a component to Mercury's precession that arises from the gravitational tugs exerted by Jupiter and the other massive planets.) In the GW signal, the periastron precession introduces an additional modulation frequency to the sound.
- Like circular orbits, elliptical orbits experience radiation reaction--the orbits decay as GWs are emitted, causing the separation to shrink with the orbit frequency increasing. However, the ellipticity of the orbit modifies this process. The binary shrinks at a faster rate when it is more elliptical. Further, as the binary shrinks the ellipticity of the orbit also gets smaller--the GW emission tends to circularize the orbit.
Non-evolving orbits
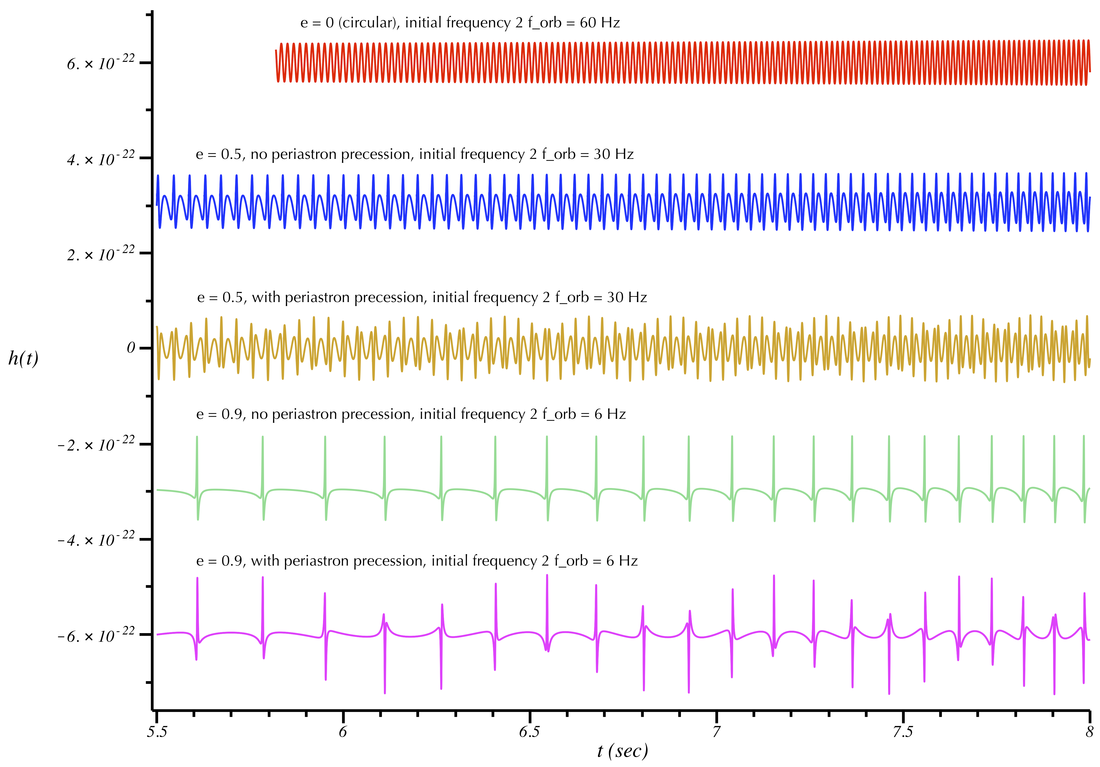
Let's investigate some of these effects. First, let's artificially turn off radiation-reaction; i.e., we'll assume that the binary orbits do not shrink in response to their GW emission. Here is what the GW signal looks like in this scenario for different values of the ellipticity e. We also experiment with turning the periastron precession effect on or off.
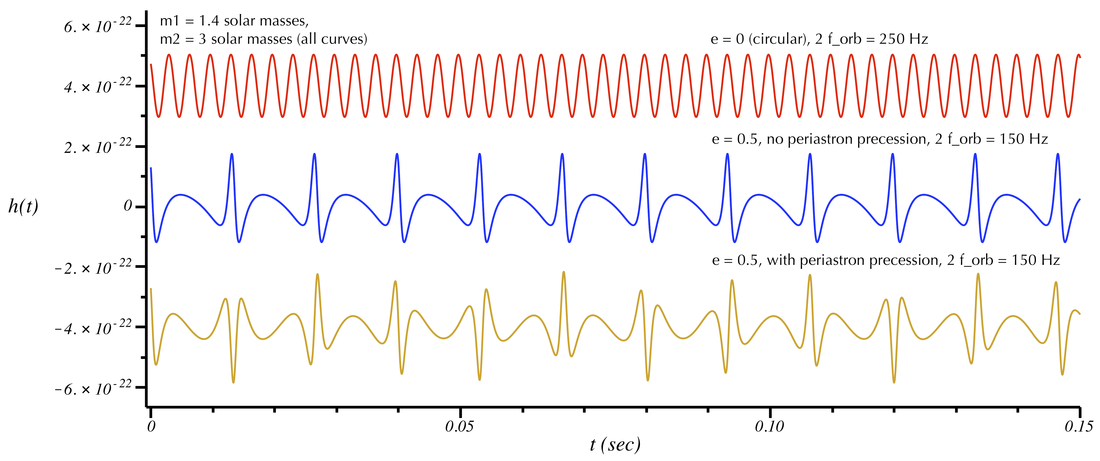
GW signal from non-shrinking neutron star + black hole binary. Two ellipticities are shown: e=0 (circular/top/red) and e=0.5 (middle/blue and bottom/gold). In the blue curve we have turned the periastron precession effect off. It is turned on in the gold curve. The corresponding sounds are below. Because eccentricity significantly modifies the frequency content of the signal and sounds, it was necessary to show signals corresponding to different orbital frequencies (f_orb is the orbital frequency; 2 f_orb would be the strongest frequency component if the orbit were circular).
Similar to the above plot except only showing e=0.9 with periastron precession off (top/green) or on (bottom/magenta). Notice the extreme "spikiness" of the signal when the orbit is highly elliptical. Notice also that an additional modulation is present due to periastron precession.
Same plot as above but zoomed-in to resolve the sharp spiky features.
Examine the plots and their corresponding sounds. (The sounds do not vary, so you only need to listen for 2 or 3 seconds.) The circular orbit (red) is a pure tone. When adding eccentricity (e=0.5, blue curve) you clearly notice that there is now more "structure." (Note that the orbital frequency has been lowered so that the resulting sound---which now includes frequency components several times the orbit frequency---is less annoying to listen to.) Turning on periastron precession (gold curve), you hear further structure (i.e. frequency components) are being added to the signal. Finally, when the eccentricity gets quite large (e=0.9, green curve) the distinct "knocking" sound becomes very apparent; adding precession to this introduces an interesting modulation to the knocking.
Evolving elliptical binaries
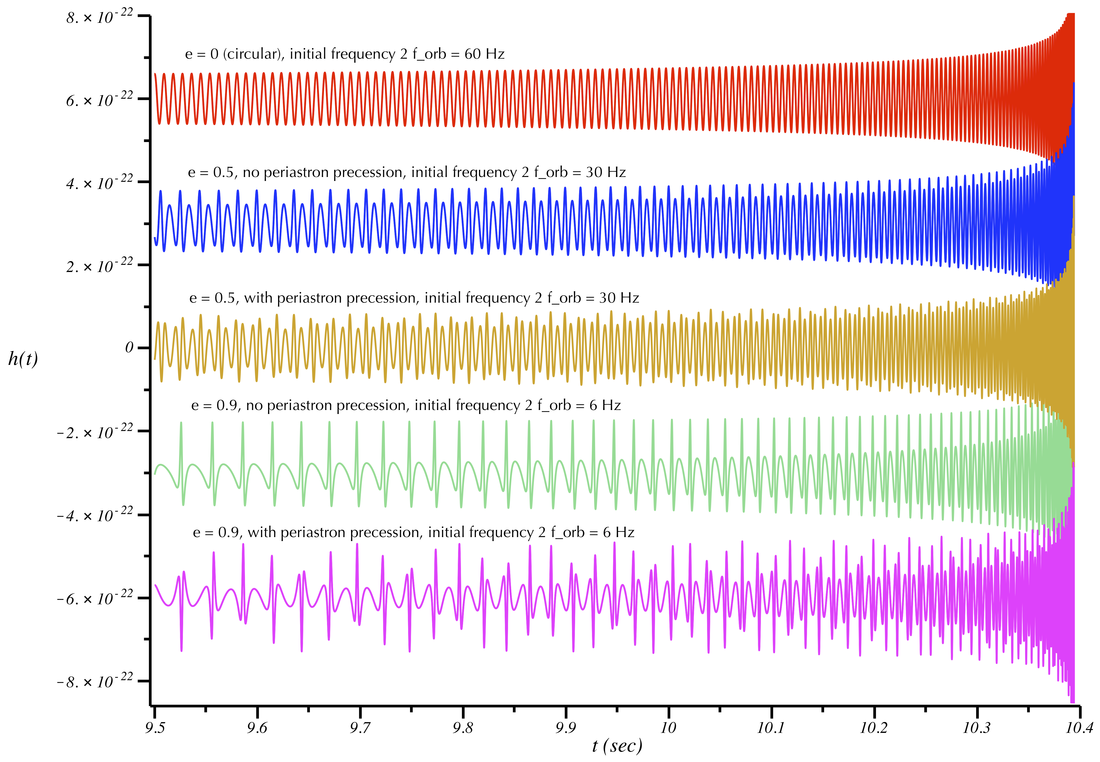
Now let's turn radiation-reaction on, allowing the orbits to shrink and the orbital frequency to increase with time. As in the circular case, the frequencies present in the sounds will increase with time along with the increase in amplitude. The cases we examine below are similar to the non-evolving cases we looked at above, but we have adjusted the starting orbital frequency to produce sounds that evolve at an appropriate rate, clearly display the relevant features, and are not too annoying to the ear. Examine the behavior of the different cases below and listen to the corresponding sounds.
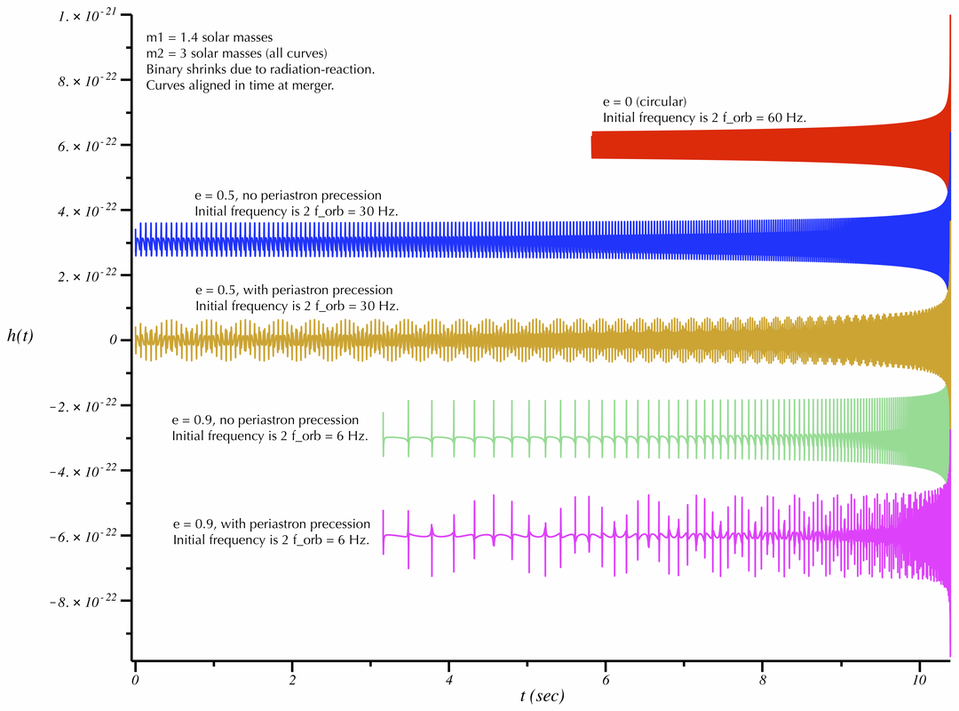
1.4 solar mass neutron star inspiralling into a 3 solar mass black hole. The orbit ellipticity is varied, as well as the presence or absence of periastron precession. The binary shrinks due to gravitational-wave emission, and the ellipticity decreases as the inspiral progresses. (The indicated ellipticity is the value at the starting time.) The signals start at different orbital frequencies and are time-shifted to line up at the merger time.
Same as above but zooming in to show the early-time structure of the signal. Notice that the frequency is increasing as time progresses (the time difference between adjacent peaks is getting smaller).
Same as above but zooming in to show the final second before merger.
Listen to the sounds above and compare to the plots of the gravitational-wave signals. Notice that many of the features from the non-evolving case remain. When radiation reaction is present, you can hear the all the frequencies present in the sound sweep up to higher values. As the volume of the sound increases the ellipticity of the binary decreases---this is illustrated by a decrease in the "knocking" component of the signal. Because the ellipticity is decreasing, the elliptical binaries sound closer to the circular case as the approach the end of the inspiral.
What if the black holes rotate about their own axes? How does that affect the gravitational wave signal? Learn more at our spinning binaries page.
What if the black holes rotate about their own axes? How does that affect the gravitational wave signal? Learn more at our spinning binaries page.
Notes on waveform model used to produce sounds on this page:
The sounds on this page used a simplified waveform model. The amplitude and phasing are accurate only to leading post-Newtonian order (0PN). When periastron precession is neglected, Newtonian elliptical orbits are used. Periastron precession is accounted for by adding a 1PN accurate periastron term to the relevant equation of motion. The compact objects are nonspinning and assumed to lie 100 Mpc from Earth. Sky localization angles in the detector antenna pattern functions are taken to be Theta=Phi=0. The polarization angle is Psi=pi/8. The binary inclination angle is pi/8. Only the inspiral is considered and the calculation is stopped at an upper frequency corresponding to the last stable orbit (ISCO). For details see Eqs. 2.12, 2.14-2.23, 2.29, and 2.36 of Favata, Phys. Rev. D 84, 124013 (2011).
The sounds on this page used a simplified waveform model. The amplitude and phasing are accurate only to leading post-Newtonian order (0PN). When periastron precession is neglected, Newtonian elliptical orbits are used. Periastron precession is accounted for by adding a 1PN accurate periastron term to the relevant equation of motion. The compact objects are nonspinning and assumed to lie 100 Mpc from Earth. Sky localization angles in the detector antenna pattern functions are taken to be Theta=Phi=0. The polarization angle is Psi=pi/8. The binary inclination angle is pi/8. Only the inspiral is considered and the calculation is stopped at an upper frequency corresponding to the last stable orbit (ISCO). For details see Eqs. 2.12, 2.14-2.23, 2.29, and 2.36 of Favata, Phys. Rev. D 84, 124013 (2011).
