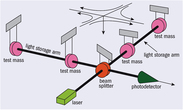
What are gravitational waves?

Gravitational waves are oscillations in the gravitational field. Just as the accelerated motion of electric charges or magnets produces electromagnetic waves, the accelerated motion of masses produces gravitational waves (which also propagate at the speed of light). Gravitational waves (GWs) are predictions of General Relativity--Einstein's geometric description of gravity. According to relativity, massive objects deform the geometry of space and time. The gravitational influence arises when other objects move on this deformed geometry. When a massive object moves rapidly back and forth, it produces ripples in this geometry which propagate away from the object. It is these ripples that LIGO has finally detected.

While any non-spherical, accelerating motion of masses produces GWs, the strongest sources are expected to be pairs of orbiting compact objects: black holes, neutron stars, or white dwarfs in a close binary. These remnants of stellar explosions are incredibly dense concentrations of matter and energy that move at relativistic speeds (close to the speed of light). They produce significant GWs which carry energy away from the binary, causing the separation between the two stars to shrink. Besides compact-object binaries, other potential sources of GWs are supernova explosions, single deformed neutron stars, and the Big Bang itself.

We know that GWs exist because we have observed the orbital decay of binary pulsars. These systems contain a rapidly spinning neutron star (emitting a bright radio pulse that sweeps over the Earth) and another compact object (a white dwarf or another neutron star). For some of these systems we observe the orbit separation shrinking at precisely the rate predicted by energy loss due to GW emission. The first of these systems (PSR B1913+16) led to a Nobel Prize for its discoverers.

While the radio signals from pulsar binaries provide some indirect knowledge about GWs, if we could directly detect GWs passing through the Earth, we would learn about all sorts of astrophysical systems that are too dim to be seen with electromagnetic waves. For example, we will see all those binary neutron stars that don't happen to have a radio beam directed at the the Earth. We'll see black hole binaries that emit very little light. From those observations we can determine the masses and spins of the black holes or neutron stars and determine how often these object merge together (which is affected by many processes in stellar evolution). We will also probe properties of the ultradense matter inside a neutron star and determine if black holes obey Einstein's precise mathematical prescription. Besides merging neutron stars or black holes, LIGO could also detect exploding stars (supernovae), single deformed neutron stars, cosmic strings, echos from the Big Bang, or something entirely unexpected. Exciting stuff!

So, how can we detect GWs? We use a device called a laser interferometer to measure the oscillating curvature of space and time as the GW passes the Earth. More specifically, the laser interferometer in LIGO is a large L-shaped device, with suspended mirrors at the ends of each "arm" of the "L." Laser light bounces inside these cavities and measures the very tiny differences in their lengths as a GW shrinks one arm and stretches the other. In the initial version of LIGO, we could detect stretching/squeezing of the arms as small as 1/1000th the diameter of a proton. (That's really, really, really small.) However, GW sources that would produce a signal that large are actually quite rare, so we had to build a better detector---Advanced LIGO---which is 10 times more sensitive and 1000 times more likely to detect GW events. The advanced detectors are now installed and began taking data in the later half of 2015. The first detection happened on September 14, 2015.

Still, the problem of finding GWs remains very difficult because lots of things will disturb the detector and could look like GWs. That's why there are two LIGO detectors--a strong signal in one detector should be seen in the other. We are also aided in our search by a process called matched filtering. This allows us to pick out a weak signal from the detector noise if we have an accurate model or template. These templates are mathematical models of the GW signal that are determined by solving Einstein's equations. 

The purpose of this site is to explore these GW template models for different physical systems by converting them to sound files. In particular, we want to learn how changing the parameters of the model affects the signal and its corresponding sound. We hope this will give you a better understanding of the interesting information that is contained in these signals.

Figure credits (top of page to bottom): NASA, Einstein by Oren Turner, NANOgrav, M. Kramer, NASA, Mezzacappa, LIGO, LIGO.