GW170104: the third confirmed detection
On June 1, 2017, the LIGO Scientific Collaboration (LSC) and Virgo collaboration announced the third confirmed detection of gravitational waves from the merger of two black holes. Here are some of the key facts from this discovery.
Key Facts about GW170104
Key Facts about GW170104
- The signal was detected on January 4, 2017 at 5:12AM Eastern Time and is hence named GW170104. The waves arrived first at the Hanford detector and 3 milliseconds later at the Livingston detector. The signal was localized to within ~1200 square degrees---an area ~6000 times larger than the full Moon.
- The gravitational waves were produced by two black holes with masses of about 31.2 and 19.4 solar masses. They merged to produce a single black hole with a mass of 48.7 solar masses. About 2.0 solar masses was released in gravitational-wave energy (comparable to the amount of energy released in the other detections).
- The signal originated about 3 billion light years away. However, the distance determination has a large error (of order ~50%) and can span a range (at 90% confidence) between 1.6 billion and 4.3 billion light years. GW170104 is most likely ~twice as far as the two confirmed detections (GW150914 and GW151226), but not as far as the less-confident signal LVT151012.
- The signal was observed with a network signal-to-noise ratio (SNR) of 13 (comparable to the SNR for GW151226). An estimate of the background event rate (e.g., due to detector glitches) indicates a false alarm rate of less than 1 in 70,000 years. The probability that this event is of astrophysical origin is estimated to be 99.997%.
- Estimates of certain combinations of the black hole spin parameters indicates that large spins that are aligned with the orbital angular momentum are unlikely. The possibility that both spins are zero is not excluded. The spin of the final black hole formed is 0.64 of the maximum value, which is similar to the other detected events. See more information about the spin below.
- As with the other detections, the signal is fully consistent with Einstein's general relativity. For this event, better tests for violations of Lorentz invariance were performed (due to the likely larger distance of this event); no violations were found. This is discussed in more detail below, including "sounds" that try to illustrate how Lorentz invariance violations affect a gravitational-wave signal.
- Combined with the other detections, GW170104 provides further evidence for a population of heavy stellar-mass black holes (>20 solar masses). Such black holes would have likely been formed from massive stars with a lower "metal" content than our sun (where here
"metal" means elements with larger atomic numbers than hydrogen and helium). The absence of large-aligned spins could be hinting that the binary formed in a very dynamical environment (like a globular cluster)---involving multibody gravitational interactions. But the data are also consistent with binaries formed in isolation (i.e., from two massive stars that formed a binary long before they became black holes.)
Below we show an interesting computer simulation of these events and look at some of the plots from the publication. And of course we explore sounds from GW170104---comparing the data to the templates. We also compare the sounds from all the observed detections so far. Lastly, we discuss the phenomenon of Lorentz violation and how LIGO was able to put constraints on it.
- LIGO.org detection page on GW170104
- Science Summary for GW170104
- Discovery paper at Physical Review Letters and companion Physics Synopsis article.
- Fact sheet on GW170104.
- Caltech press announcement on GW170104.
- New York Times article on the discovery.
- LIGO Open Science Center (LOSC) site for GW170104.
The "Sound" of GW170104
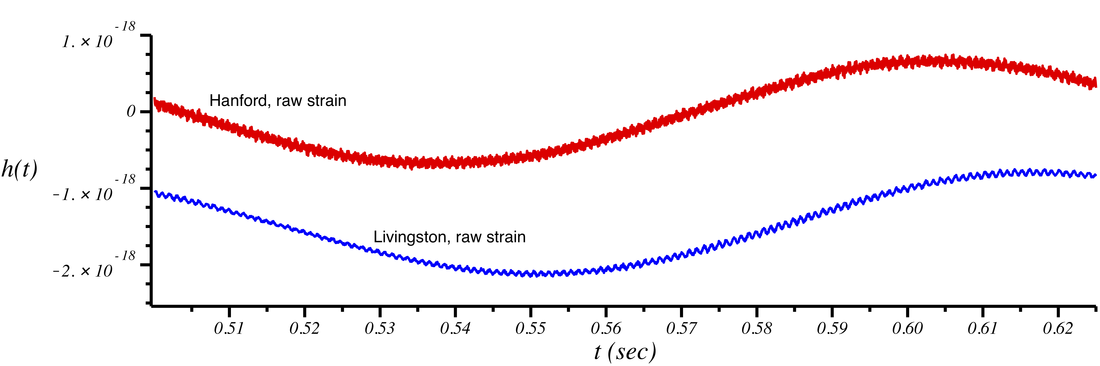
Now, let's explore the GW170104 signal and the corresponding audio. First let's look at a stretch of the raw (unprocessed) strain produced by each detector (Hanford/red, Livingston/blue) during the time period when GW170104 is in the detector frequency band. "Strain" refers to the length difference between the two arms of a LIGO interferometer, divided by the total length (4km); it is the primary observable in LIGO measurements. As we see below, the raw strain is dominated by the instrument noise---none of the wiggles you see in the plot below are the GW170104 signal (but the signal is buried "in there").
Unprocessed strain data from LIGO Hanford and Livingston detectors, during the time GW170104 was detected. [Data here and in the following related plots are courtesy of James Clark and the LIGO team.]
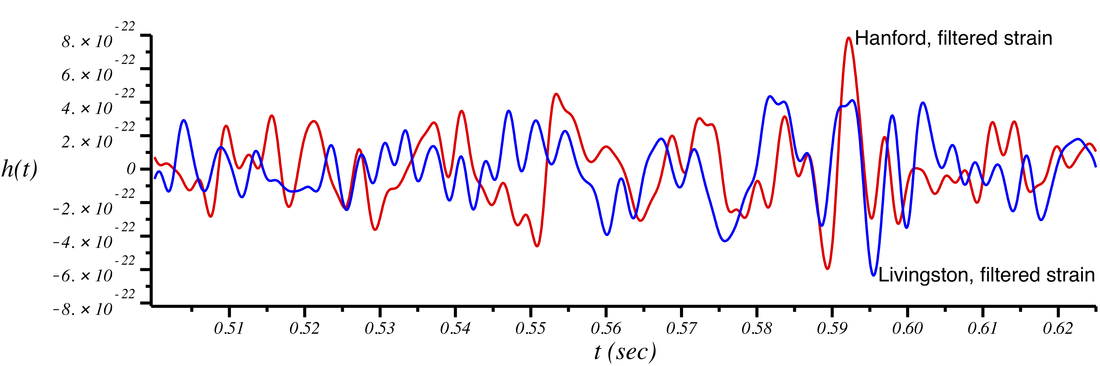
To actually see the signal, one can apply a "filter" to the above data. If the detector output is sampled over a longer period (when there are likely few detectable signals), one can compute a noise spectrum and use it to filter out the noise in the above stretch of data. Essentially, this removes frequencies where the detector noise is loud and allows the signal to become visible. (See the nice LOSC tutorials for more information.) The corresponding stereo audio is below the plot.
LIGO data processed through a filter to make the GW170104 signal visible. (Hanford/red, Livingston/blue.)
Now you can clearly hear a short but characteristic "chirp" sound corresponding to GW170104 (along with a bit of residual noise that survived the filter). Notice the scale difference in the y-axis between the "raw strain" (\( \sim 10^{-19} \)) and the filtered strain (\( \sim 10^{-22} \)) ---a factor of 1000 difference!!
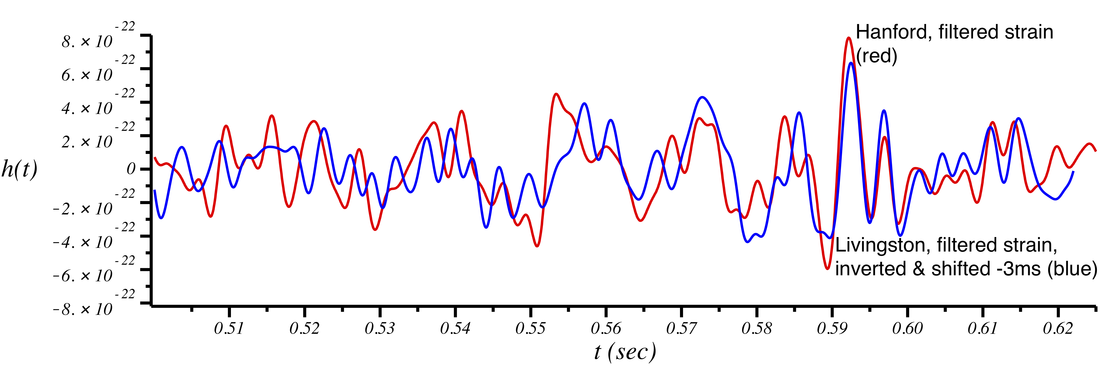
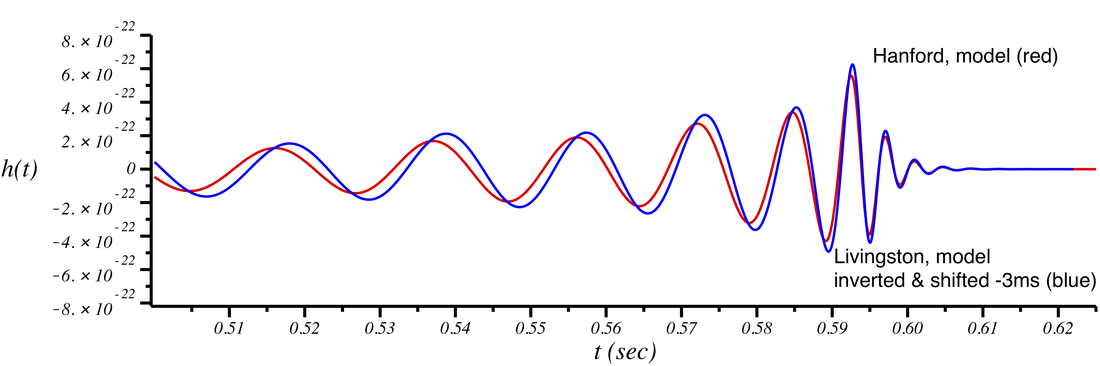
Notice that the signals from Hanford and Livingston don't line up especially well. This is because the detectors are oriented differently and because there was a 3 ms time delay for the signal to reach Livingston after passing through the Hanford detector. In the plot below, we multiply the Livingston signal by -1 (accounting for the relative rotation of the two detectors) and shift it 3 ms earlier in time:
Notice that the signals from Hanford and Livingston don't line up especially well. This is because the detectors are oriented differently and because there was a 3 ms time delay for the signal to reach Livingston after passing through the Hanford detector. In the plot below, we multiply the Livingston signal by -1 (accounting for the relative rotation of the two detectors) and shift it 3 ms earlier in time:
Same as above plot but with Livingston (blue) curve inverted and shifted by 3ms.
Now the signals from each detector line up much more nicely, indicating that a consistent signal occurred in each interferometer.
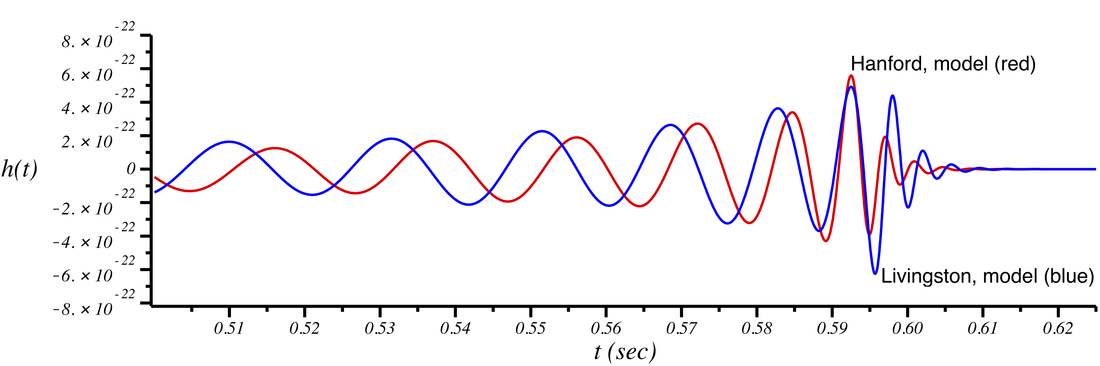
The signal model (the gravitational-wave signal itself, with no detector noise at all) looks and sounds like the following:
The signal model (the gravitational-wave signal itself, with no detector noise at all) looks and sounds like the following:
Signal model consistent with the parameters for GW170104. This includes the effect of the "antenna pattern" for each detector.
If we again invert the Livingston signal model and time shift it, we get model signals in each detector that line up very nicely:
Same as above but with Livingston signal (blue) inverted and shifted by 3ms.
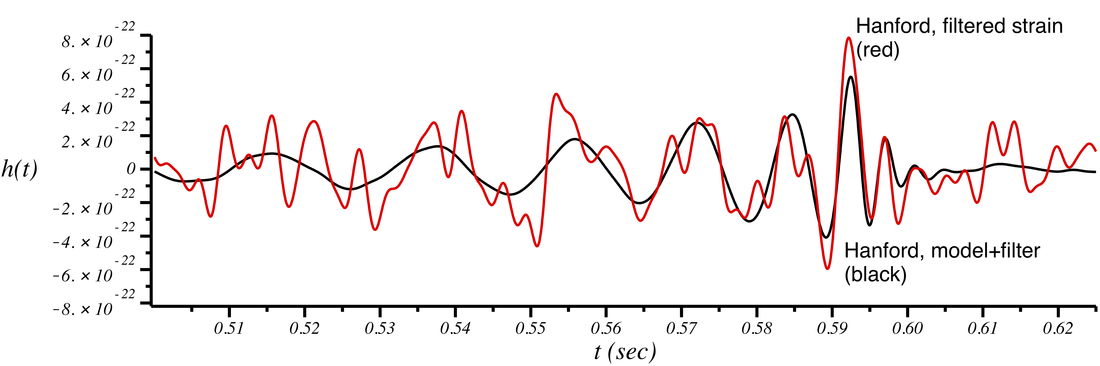
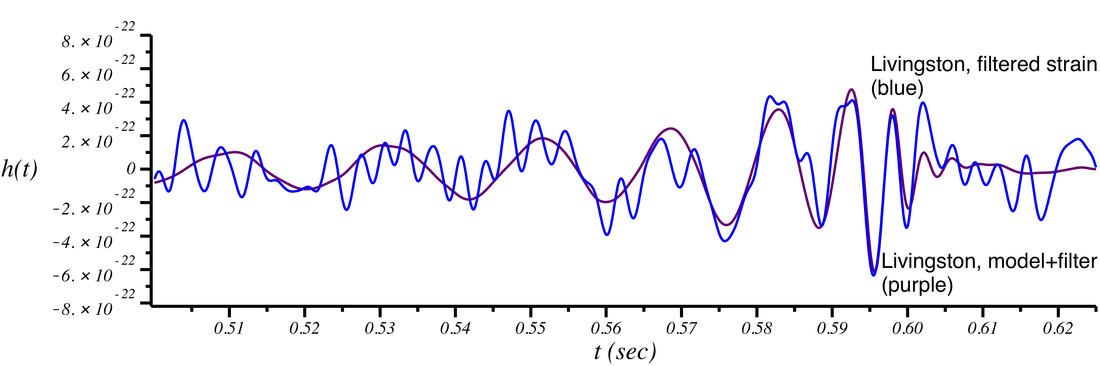
As a final comparison, we can take the signal model in each detector, apply the same filter to it that was applied to the raw strain, and plot it on top of the filtered strain. The result is the following:
Comparison of the filtered data from Hanford (red) and the waveform model projected onto the Hanford detector with the same filter applied (black).
Same as above, but for Livingston filtered data (blue) and model (purple).
We see good agreement between the model and the filtered data. There is clearly a gravitational-wave model underneath that detector output. If the filtered model is subtracted from the filtered data, the result is consistent with detector noise. This is what is shown in figure 1 of the discovery paper.
Sounds from GW170104 and other LIGO detections are also available at the LSOC data release page.
Sounds from GW170104 and other LIGO detections are also available at the LSOC data release page.
"Sounds" from first four LIGO events
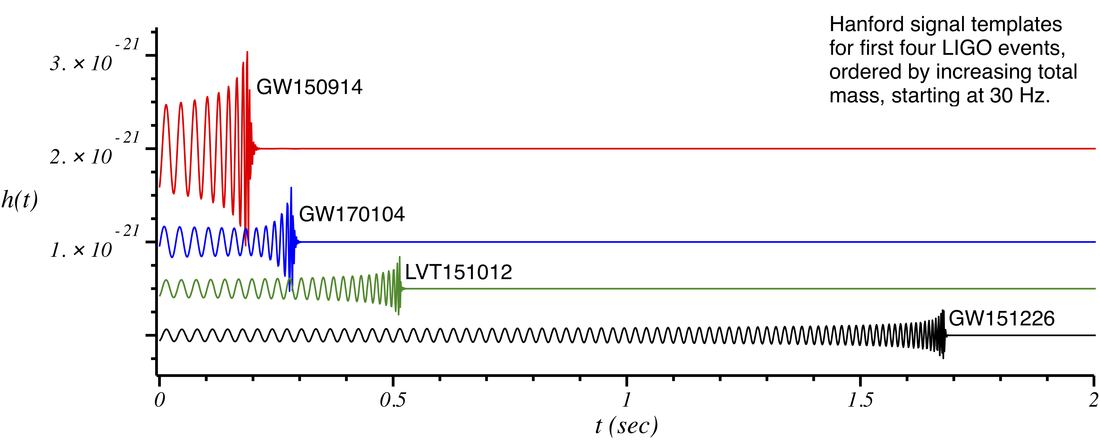
Let's compare the signals and sounds from the first four LIGO events. The plot below shows the waveform models projected in the Hanford detector. What is plotted is not data but a kind of "most probable" waveform model for each event (accounting for the Hanford antenna pattern function). The signals are shown starting from 30 Hz. (The actual sensitivity of the detector goes down to ~20 to 25Hz, but the audible sound below 30 Hz is difficult to perceive unless your speakers have very good low frequency response; human ears also have difficulty perceiving such low frequencies.) The signals are ordered by increasing total mass (bottom to top of figure). Notice that as the mass increases, the signals get shorter, louder, and stop at lower frequencies. More massive binaries produce stronger gravitational waves, but because those black holes are larger, the final binary orbit separation is larger (resulting in lower frequencies). This is also a generic property of sound produced by mechanical systems: larger systems typically produce lower-frequency sounds. (Think of a large diameter drum vs. a small drum, or a long bass string vs. a short violin string.)
Below the figure are stereo sounds corresponding to the events shown (with the Hanford signal in the left channel, Livingston in the right; note that the Livingston data is not shown in the plot but is qualitatively similar). The first sound plays all four events in sequence from top to bottom in the plot (starting with GW150914). The volume is in direct proportion to the relative signal amplitudes (so GW151226 has the lowest volume but is longer and reaches the highest frequencies). The remaining four files are the separate events individually, but without the volume scaled relative to each other. Notice how the frequency and duration changes with mass.
Below the figure are stereo sounds corresponding to the events shown (with the Hanford signal in the left channel, Livingston in the right; note that the Livingston data is not shown in the plot but is qualitatively similar). The first sound plays all four events in sequence from top to bottom in the plot (starting with GW150914). The volume is in direct proportion to the relative signal amplitudes (so GW151226 has the lowest volume but is longer and reaches the highest frequencies). The remaining four files are the separate events individually, but without the volume scaled relative to each other. Notice how the frequency and duration changes with mass.
Hanford waveform models for all LIGO events so far, ordered by increasing total mass (lower masses on bottom). [Data courtesy of Ben Farr and the LIGO team.]
Masses & Spins
Let's take a look at some interesting plots related to the estimated masses and spins of GW170104.
First we see two plots that compare the masses of all the detected signals.
First we see two plots that compare the masses of all the detected signals.
The left chart shows the masses of the black holes detected by LIGO (blue) before and after they merged. Notice how much larger they are than those stellar-mass black holes that were discovered using x-ray observations (purple). In particular, GW170104 and GW150914 are clearly showing that there is a population of stellar-mass black holes above 20 solar masses. The right plot shows the probability density for each mass component (\(m_1, m_2\)) of GW170104, with clear peaks near 20 and 30 solar masses. The middle of that plot shows probability contours for all the LIGO detections (at 50% and 90% confidence for the inner/outer contours). Notice that GW170104 lies in-between GW150914 and LVT151012; its masses are measured to a precision of ~20% to 30%. The \(m_1-m_2\) contours are banana-shaped because the signal templates depend on a particular combination of the masses called the "chirp mass"---it is that combination that is most easily measured by LIGO, not \(m_1\) and \(m_2\) individually. That is why the contours are narrow along one direction and elongated along the other. For GW151226, the contour is especially narrow---this is because that system had many more observable wave cycles during the inspiral, which allowed the chirp mass to be measured very precisely for that system. (Nonetheless, because other parameters that are intertwined with the masses were not measured precisely, the individual masses for GW151226 are not actually known with higher precision, as can be seen by the projection of that skinny contour along the \(m_1\) or \(m_2\) axes.)
In the pair of plots below (also from the journal publication of the discovery) we investigate what we learned about the black hole spins:
In the pair of plots below (also from the journal publication of the discovery) we investigate what we learned about the black hole spins:
The left figure shows a "polar-like" plot where the radial distance from the center represents the dimensionless spin magnitude \(\chi_i \equiv c |{\mathbf S}_i|/(G m_i^2), \, i=1,2\), for each black hole (larger mass \(m_1\) on the left side, the smaller mass \(m_2\) on the right). This spin parameter \(\chi_i\) varies from 0 to 1. The colored region shows the probability density as a function of the spin magnitude (radial direction) and the angle \(\theta\) that the corresponding spin vector \({\mathbf S}_i\) makes with respect to the orbital angular momentum \({\mathbf L}\). We see that there is very little probability for the case where the two spin vectors are both large (bigger than ~0.4) and nearly aligned (theta ~0 to 30 degrees). On the other hand, the dark purple region (the more probable area) shows evidence for misalignment.
The right figure shows the probability density for the "effective spin parameter" \(\chi_{\rm eff}\) for all the known detections so far. This parameter is a mass-weighted sum of each of the spin vectors \({\mathbf S}_i\) projected along the orbital angular momentum (\({\mathbf L}\)) direction. For example, this parameter might be large and positive if both spins are nearly aligned with \({\mathbf L}\) and large. But it might be small if (i) each spin is large but one is aligned with \({\mathbf L}\) and the other anti-aligned, or (ii) if both are large and pointing in the plane of the orbit (90-degrees from \({\mathbf L}\)), or (iii) if both spins are small. For GW150914 and LVT151012, the figure indicates that the black hole spins are not very large and aligned or anti-aligned with \({\mathbf L}\); they could be both small, or large but oriented in such a way that a cancellation occurs when \(\chi_{\rm eff}\) is computed. For GW151226, we see that \(\chi_{\rm eff}\) is clearly positive and non-zero; this means at least one of the spins is not small and has a significant component along \({\mathbf L}\). For GW170104, we see a preference for \(\chi_{\rm eff} < 0 \) (but \(\chi_{\rm eff} = 0 \) is not excluded). This favors (but does not compel) a scenario in which at least one of the spins is modest and pointing >90 degrees away from \({\mathbf L}\) (as indicated in the left plot).
The right figure shows the probability density for the "effective spin parameter" \(\chi_{\rm eff}\) for all the known detections so far. This parameter is a mass-weighted sum of each of the spin vectors \({\mathbf S}_i\) projected along the orbital angular momentum (\({\mathbf L}\)) direction. For example, this parameter might be large and positive if both spins are nearly aligned with \({\mathbf L}\) and large. But it might be small if (i) each spin is large but one is aligned with \({\mathbf L}\) and the other anti-aligned, or (ii) if both are large and pointing in the plane of the orbit (90-degrees from \({\mathbf L}\)), or (iii) if both spins are small. For GW150914 and LVT151012, the figure indicates that the black hole spins are not very large and aligned or anti-aligned with \({\mathbf L}\); they could be both small, or large but oriented in such a way that a cancellation occurs when \(\chi_{\rm eff}\) is computed. For GW151226, we see that \(\chi_{\rm eff}\) is clearly positive and non-zero; this means at least one of the spins is not small and has a significant component along \({\mathbf L}\). For GW170104, we see a preference for \(\chi_{\rm eff} < 0 \) (but \(\chi_{\rm eff} = 0 \) is not excluded). This favors (but does not compel) a scenario in which at least one of the spins is modest and pointing >90 degrees away from \({\mathbf L}\) (as indicated in the left plot).
The "sound" of Lorentz invariance violation
What the heck is Lorentz invariance? It is a key feature of Einstein's theory of special relativity that is incorporated into all relativistic theories (like general relativity and quantum field theories). It says that the laws of physics obey a certain symmetry involving space and time: no particular direction in space is preferred, no observer's clock is more special than any other, and all inertial frames are equivalent. (Different inertial frames correspond to different observers moving with constant velocity with respect to each other.) When space and time coordinates are transformed according to a particular mathematical law (the Lorentz transformation), physical laws have the same mathematical form in the new coordinate system. The laws of physics as we understand them today obey this local Lorentz invariance. ("Local" because this symmetry only applies on scales small enough where spacetime can be approximated as flat.)
Why would this be violated? The violation potentially arises in theories motivated by attempts to combine quantum mechanics and gravity. These theories predict that at very small length or time scales (of order the Planck length or Planck time), corrections to general relativity (GR) become important. Because these modifications "turn on" at this Planck scale, there is a "preferred scale"---whereas in local Lorentz invariant theories there is no preferred scale at all. Hence, we have local Lorentz violation in these theories. The details of how this Lorentz violation works varies from theory to theory; but there are generic predictions for how this affects the propagating "modes" of a theory. One generic prediction is vacuum dispersion: different frequencies of electromagnetic waves or gravitational-waves will propagate through empty space at different speeds. In the standard Maxwell equations or Einstein equations, all frequencies of electromagnetic waves or gravitational waves move through the vacuum at the same speed, \(v=c=2.9979\ldots \times 10^8\) m/s. When these waves propagate through matter, dispersion does occur: that's why we see rainbows, refraction, or the dispersion of light into colors by a prism. In theories that break local Lorentz invariance, dispersion also happens when propagating through the vacuum.
There are different ways of trying to observe this, and one way involves using gravitational-waves. The fact that different frequencies will move at different speeds implies an evolving phase correction to the waveform of a gravitational-wave signal. This is the effect that LIGO looked for when analyzing the data from GW170104. The magnitude of this phase difference is proportional to the distance that the waves have to travel. Since GW170104 was probably the furthest LIGO event so far, this allowed a better test of local Lorentz violation than the other events. No violations of local Lorentz invariance were found.
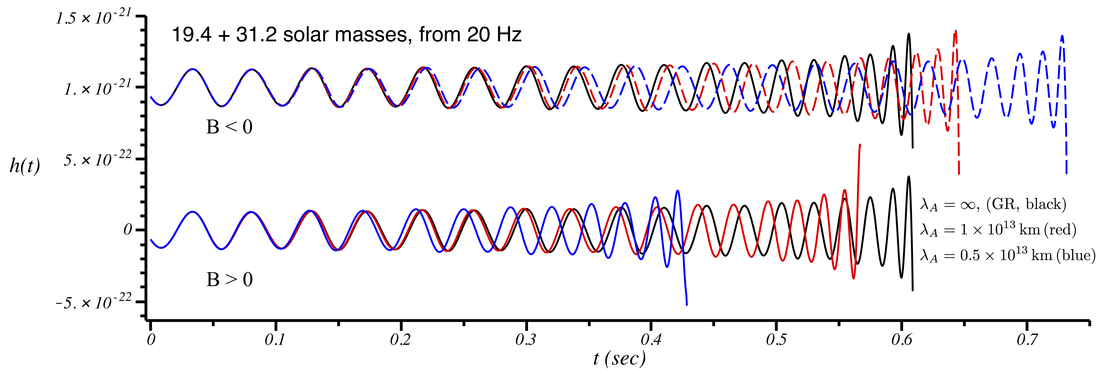
To give an example of how local Lorentz invariance violation affects the gravitational-wave signal, we modeled the inspiral-only part of a gravitational-wave signal for several choices of a parameter that "dials" up or down the size of the Lorentz violation. This parameter \(\lambda_A\) is a length scale related to the energy scale of Lorentz violation. The effect is proportional to a constant \(B \propto \pm M D/\lambda_A^2\), where \(D\) is (approximately) the binary distance, \(M\) is the total binary mass, and the sign (\(\pm\)) of \(B\) corresponds to sub-luminal (\(B > 0\)) or superluminal (\(B < 0\)) propagation of the gravitational waves. For \(B > 0\) this can be related to a theory in which the graviton has a non-zero mass. [In this case, \(\lambda_A\) is the Compton wavelength of the graviton, \(\lambda_A=h/m_g c\), where \(h\) is Planck's constant and \(m_g\) is the graviton mass]. The parameter \(\lambda_A\) is infinite in general relativity (corresponding to zero graviton mass if \(B > 0\)). Smaller \(\lambda_A\) makes the Lorentz violation effect bigger (e.g., larger graviton mass). (See the technical note at the bottom of this page for more details.)
In the first plot below, we show the effect of local Lorentz invariance on the waveform of a binary with masses similar to GW170104. The two black curves are identical and represent the general relativity (GR) case. The red and blue curves show the indicated value of \(\lambda_A\). The subluminal (\(B>0\)) and superluminal (\(B<0\)) cases are vertically offset from each other. The waves with Lorentz violation become out of phase with the GR case. We see that the effect of lowering \(\lambda_A\) from the GR value is to make the effect larger. (Note that the GW170104 paper placed the constraints \(\lambda_A > 1.3 \times 10^{13}\) km for \(B>0\) and \(\lambda_A > 6.6 \times 10^{12}\) km for \(B<0\); see Table III of the supplemental materials; the choices here are in the same ballpark and make for an illustrative plot.)
Why would this be violated? The violation potentially arises in theories motivated by attempts to combine quantum mechanics and gravity. These theories predict that at very small length or time scales (of order the Planck length or Planck time), corrections to general relativity (GR) become important. Because these modifications "turn on" at this Planck scale, there is a "preferred scale"---whereas in local Lorentz invariant theories there is no preferred scale at all. Hence, we have local Lorentz violation in these theories. The details of how this Lorentz violation works varies from theory to theory; but there are generic predictions for how this affects the propagating "modes" of a theory. One generic prediction is vacuum dispersion: different frequencies of electromagnetic waves or gravitational-waves will propagate through empty space at different speeds. In the standard Maxwell equations or Einstein equations, all frequencies of electromagnetic waves or gravitational waves move through the vacuum at the same speed, \(v=c=2.9979\ldots \times 10^8\) m/s. When these waves propagate through matter, dispersion does occur: that's why we see rainbows, refraction, or the dispersion of light into colors by a prism. In theories that break local Lorentz invariance, dispersion also happens when propagating through the vacuum.
There are different ways of trying to observe this, and one way involves using gravitational-waves. The fact that different frequencies will move at different speeds implies an evolving phase correction to the waveform of a gravitational-wave signal. This is the effect that LIGO looked for when analyzing the data from GW170104. The magnitude of this phase difference is proportional to the distance that the waves have to travel. Since GW170104 was probably the furthest LIGO event so far, this allowed a better test of local Lorentz violation than the other events. No violations of local Lorentz invariance were found.
To give an example of how local Lorentz invariance violation affects the gravitational-wave signal, we modeled the inspiral-only part of a gravitational-wave signal for several choices of a parameter that "dials" up or down the size of the Lorentz violation. This parameter \(\lambda_A\) is a length scale related to the energy scale of Lorentz violation. The effect is proportional to a constant \(B \propto \pm M D/\lambda_A^2\), where \(D\) is (approximately) the binary distance, \(M\) is the total binary mass, and the sign (\(\pm\)) of \(B\) corresponds to sub-luminal (\(B > 0\)) or superluminal (\(B < 0\)) propagation of the gravitational waves. For \(B > 0\) this can be related to a theory in which the graviton has a non-zero mass. [In this case, \(\lambda_A\) is the Compton wavelength of the graviton, \(\lambda_A=h/m_g c\), where \(h\) is Planck's constant and \(m_g\) is the graviton mass]. The parameter \(\lambda_A\) is infinite in general relativity (corresponding to zero graviton mass if \(B > 0\)). Smaller \(\lambda_A\) makes the Lorentz violation effect bigger (e.g., larger graviton mass). (See the technical note at the bottom of this page for more details.)
In the first plot below, we show the effect of local Lorentz invariance on the waveform of a binary with masses similar to GW170104. The two black curves are identical and represent the general relativity (GR) case. The red and blue curves show the indicated value of \(\lambda_A\). The subluminal (\(B>0\)) and superluminal (\(B<0\)) cases are vertically offset from each other. The waves with Lorentz violation become out of phase with the GR case. We see that the effect of lowering \(\lambda_A\) from the GR value is to make the effect larger. (Note that the GW170104 paper placed the constraints \(\lambda_A > 1.3 \times 10^{13}\) km for \(B>0\) and \(\lambda_A > 6.6 \times 10^{12}\) km for \(B<0\); see Table III of the supplemental materials; the choices here are in the same ballpark and make for an illustrative plot.)
Waveforms showing varying Lorentz invariance violation. The black waveforms are identical and represent the general relativity (GR) case. Those with \(B<0\) (top) have superluminal propagation. Those with \(B>0\) (bottom) have subluminal propagation. The effect increases for smaller \(\lambda_A\).
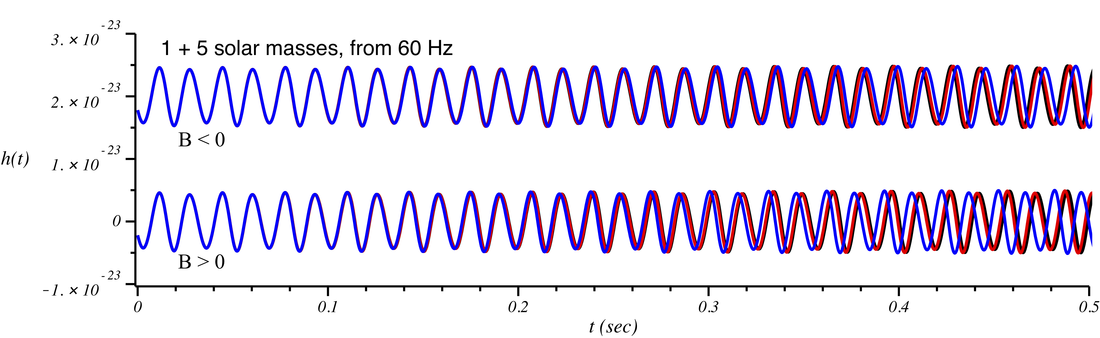
We would like to make a sound that illustrates the differences above. However, for the system illustrated in the plot above the signal duration is too short and the degree of Lorentz violation is too weak to produce easily distinguishable sounds. Instead, let's examine a different system consisting of 1 solar mass and 5 solar mass black holes (we also modify the value of \(\lambda_A\)). In this case the signal is a bit longer and Lorentz violation results in differences in duration of order ~0.5 sec (as well as an evolving phase difference). As in the case above, all signals start in phase at the same frequency (which is 60 Hz in the plots below). The second plot below shows a zoom-in of the first half-second, with the signals overlapped (as in the case above) to show the growing phase difference).
Gravitational-wave signals illustrating the effect of Lorentz violation. The central (black) waveform is the GR case. The top two show the \(B<0\) case, the bottom two show \(B>0\). The colors represents the indicated values of \(\lambda_A\). (Smaller \(\lambda_A\) increases the effect).
Same as above except we zoom-in to the first half-second and overlap the top two and bottom two curves of the previous plot with the GR case (to show the growing phase difference).
While we could make sounds of the different cases shown above to try to "hear" the effect of Lorentz invariance violation, in practice it is very difficult to hear the difference by listening to individual sounds. Instead, we produce a single sound corresponding to the GR case in the left ear, and the Lorentz-violating case in the right ear. The two sounds evolve separately and the differences become more clear when played back in this manner.
You can clearly hear in the above that the duration of the left and right channels are different (corresponding to different times it takes the signal to reach the last stable orbit frequency). More importantly, you can hear that the signals quickly grow out of phase. The effect is larger in the cases where \(\lambda_A\) is smaller.
[ Technical note for experts: The LIGO paper set constraints on a parameter \(A\). "\(A\)" is related to what we call \(\lambda_A\) above. These constraints are computed separately for different values of another parameter, \(\alpha\) (which is related to the power-law dependence of the signal frequency and varies from theory to theory). We choose \(\alpha = 0\) in the analysis here. This is equivalent to a massive-graviton theory when \(A\) or \(B\) are positive. For this \(\alpha = 0\) choice, the frequency and phase evolution of the binary gets modified at relative 1PN order; for other choices of \(\alpha\) this modification happens at higher post-Newtonian orders and is more difficult to observe---that's why the best LIGO constraints are for \(\alpha = 0\); since this choice makes the effect easiest to see, we focus on that case here. Similar (but smaller) dephasing effects will occur for \(\alpha \neq 0\). We also note that the massive graviton case where \(\alpha = 0\) and \(B\) (or \(A\)) are positive need not be Lorentz invariance violating. However, the case \(\alpha=0\) and \(A\) or \(B\) negative is Lorentz invariance violating. In other words, the \(B >0\) case shown above is technically not Lorentz violating, but corresponds to a modified dispersion relation that preserves Lorentz invariance for the gravitational degrees of freedom. Marc thanks K.G. Arun and Anuradha Samajdar for corrections that clarified the presentation in this section.
To compute the waveform models above we start with the stationary phase correction given in Eq. 6 of the PRL supplemental materials; from that we infer the frequency and phase evolution as a function of time, which we then plug into an inspiral-only circular waveform model with 2PN amplitude corrections and 3PN phase corrections. In all the cases above we assume a distance of 880 Mpc, consistent with GW170104. ]
To compute the waveform models above we start with the stationary phase correction given in Eq. 6 of the PRL supplemental materials; from that we infer the frequency and phase evolution as a function of time, which we then plug into an inspiral-only circular waveform model with 2PN amplitude corrections and 3PN phase corrections. In all the cases above we assume a distance of 880 Mpc, consistent with GW170104. ]
